Java工程师面试题-数据结构与算法

发表于 2021-11-17 更新于 2022-08-23 阅读次数：本文字数： 21k 阅读时长 ≈ 19 分钟

哈希、树、链表、数组、排序、遍历、堆栈

推荐先阅读：Java工程师面试题

哈希

请谈一谈，hashCode() 和equals() 方法的重要性体现在什么地方？

考察点：JAVA哈希表

参考回答：

Java中的HashMap使用hashCode()和equals()方法来确定键值对的索引，当根据键获取值的时候也会用到这两个方法。如果没有正确的实现这两个方法，两个不同的键可能会有相同的hash值，因此，可能会被集合认为是相等的。而且，这两个方法也用来发现重复元素。所以这两个方法的实现对HashMap的精确性和正确性是至关重要的。

请说一说，Java中的HashMap的工作原理是什么？

考察点：JAVA哈希表

参考回答：

HashMap是以键值对的形式存储元素的，需要一个哈希函数，使用hashcode和eaquels方法，从集合中添加和检索元素，调用put方法时，会计算key 的哈希值，然后把键值对存在集合中合适的索引上，如果键key已经存在，value会被更新为新值。另外HashMap的初始容量是16，在jdk1.7的时候底层是基于数组和链表实现的，插入方式是头插法。jdk1.8的时候底层是基于数组和链表/红黑树实现的，插入方式为尾插法。

介绍一下，什么是hashmap?

考察点：哈希表

参考回答：

HashMap 是一个散列表，它存储的内容是键值对(key-value)。
HashMap 继承于AbstractMap，实现了Map、Cloneable、java.io.Serializable接口。
HashMap 的实现不是同步的，所以它不是线程安全的。它的key、value都可以为null。此外，HashMap中的映射不是有序的。
HashMap 的实例有两个参数影响其性能：“初始容量” 和 “负载因子”。容量是哈希表中桶的数量，初始容量只是哈希表在创建时的容量。负载因子是哈希表在其容量自动增加之前可以达到多满的一种尺度。当哈希表中的条目数超出了加载因子与当前容量的乘积时，则要对该哈希表进行 rehash 操作（即重建内部数据结构），从而哈希表将具有大约两倍的桶数。
通常，默认加载因子是 0.75, 这是在时间和空间成本上寻求一种折衷。加载因子过高虽然减少了空间开销，但同时也增加了查询成本（在大多数 HashMap 类的操作中，包括 get 和 put 操作，都反映了这一点）。在设置初始容量时应该考虑到映射中所需的条目数及其加载因子，以便最大限度地减少 rehash 操作次数。如果初始容量大于最大条目数除以加载因子，则不会发生 rehash 操作。
HashMap在扩容的时候是2的n次幂。

讲一讲，如何构造一致性哈希算法。

考察点：哈希算法

参考回答：

先构造一个长度为2^32的整数环（这个环被称为一致性Hash环），根据节点名称的Hash值（其分布为[0, 2^32-1]）将服务器节点放置在这个Hash环上，然后根据数据的Key值计算得到其Hash值（其分布也为[0, 2^32-1]），接着在Hash环上顺时针查找距离这个Key值的Hash值最近的服务器节点，完成Key到服务器的映射查找。

这种算法解决了普通余数Hash算法伸缩性差的问题，可以保证在上线、下线服务器的情况下尽量有多的请求命中原来路由到的服务器。

请问，Object作为HashMap的key的话，对Object有什么要求吗？

考察点：哈希表

参考回答：

要求Object中hashcode不能变。

请问 HashSet 存的数是有序的吗？

考察点：哈希

参考回答：

HashSet是无序的。

树

TreeMap和TreeSet在排序时如何比较元素？Collections工具类中的sort()方法如何比较元素？

考察点：Tree

参考回答：

TreeSet要求存放的对象所属的类必须实现Comparable接口，该接口提供了比较元素的**compareTo()**方法，当插入元素时会回调该方法比较元素的大小。TreeMap要求存放的键值对映射的键必须实现Comparable接口从而根据键对元素进行排序。Collections工具类的sort方法有两种重载的形式，第一种要求传入的待排序容器中存放的对象比较实现Comparable接口以实现元素的比较；第二种不强制性的要求容器中的元素必须可比较，但是要求传入第二个参数，参数是Comparator接口的子类型（需要重写compare方法实现元素的比较），相当于一个临时定义的排序规则，其实就是通过接口注入比较元素大小的算法，也是对回调模式的应用（Java中对函数式编程的支持）。

public class
Student implements Comparable<Student> {
     private String name;        // 姓名
     private int age;            // 年龄
     public Student(String name, int age) {
         this.name = name;
         this.age = age;
     }
     @Override
     public String toString() {
         return "Student [name=" + name + ", age=" + age + "]";
     }
     @Override
     public int compareTo(Student o) {
         return this.age - o.age; // 比较年龄(年龄的升序)
     }
 }
 import java.util.Set;
 import java.util.TreeSet;
 class Test01 {
     public static void main(String[] args) {
         Set<Student> set = new TreeSet<>();     // Java 7
     }
 }
 import java.util.Set;
 import java.util.TreeSet;
 class Test01 {
     public static void main(String[] args) {
         Set<Student> set = new TreeSet<>();     // Java 7的钻石语法(构造器后面的尖括号中不需要写类型)
         set.add(new Student("Hao LUO", 33));
         set.add(new Student("XJ WANG", 32));
         set.add(new Student("Bruce LEE", 60));
         set.add(new Student("Bob YANG", 22));

         for(Student stu : set) {
            System.out.println(stu);
         }
 //      
         set.add(new Student("Hao LUO", 33));
         set.add(new Student("XJ WANG", 32));
         set.add(new Student("Bruce LEE", 60));
         set.add(new Student("Bob YANG", 22));
         for(Student stu : set) {
              System.out.println(stu);
         }
 //      输出结果: 
 //      Student [name=Bob YANG, age=22]
 //      Student [name=XJ WANG, age=32]
 //      Student [name=Hao LUO, age=33]
 //      Student [name=Bruce LEE, age=60]
     }
 }
 //      Student [name=Bob YANG, age=22]
 //      Student [name=XJ WANG, age=32]
 //      Student [name=Hao LUO, age=33]
 //      Student [name=Bruce LEE, age=60]
     }
 }

如何打印二叉树每层的节点？

考察点：二叉树

注意：面试中一般写核心代码，另外就是可以问一下面试是输出ArrayList还是int数组。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int[] levelOrder(TreeNode root) {
        // 如果root为空直接返回
        if(root == null){
            return new int[0];
        }
        // 层次遍历 
        // 队列
        Deque<TreeNode> deque = new LinkedList<>();
        // 存每一层节点
        ArrayList<Integer> temp = new ArrayList<>();
        // 根节点入队
        deque.offer(root);
        while(!deque.isEmpty()){
            int size = deque.size();
            for(int i=0;i<size;i++) {
                //层次遍历
                TreeNode curroot = deque.pop();
                temp.add(curroot.val);
                // 做节点是否为空
                if(curroot.left!=null)
                    deque.offer(curroot.left);
                if(curroot.right!=null)
                    deque.offer(curroot.right);
            }
        }
        // 如果要求返回int数组 就写上这一步，如果没有要求可以直接返回temp即可。
        int []result = new int[temp.size()];
        for(int i=0;i<result.length;i++){
            result[i] = temp.get(i);
        }
        return result;
    }
}

如何知道二叉树的深度？

考察点：二叉树

参考回答：

求二叉树的深度方式有两种，递归以及非递归。(出自剑指offer)

①递归实现：

为了求树的深度，可以先求其左子树的深度和右子树的深度，可以用递归实现，递归的出口就是节点为空。返回值为0；

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root==null) return 0;
        int left = TreeDepth(root.left);
        int right = TreeDepth(root.right);
        return (left>right)?(left+1):(right+1);
    }
}

②非递归实现：

利用层次遍历的算法，将每一层的所有节点放入队列中，在将每一层节点的左右子节点存入放入到队列中，用一个变量记录树的高度即可。

import java.util.*;
public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root==null) 
            return 0;
        Queue<TreeNode> result = new LinkedList<>();
        result.add(root);
        int height = 0;
        while(!result.isEmpty()){
            //获取当前的根节点
            int size = result.size();
            while(size>0){//遍历当前层，将该层的子节点都加入队列中
                TreeNode nowroot = result.poll();
                if(nowroot.left!=null) 
                    result.add(nowroot.left);
                if(nowroot.right!=null) 
                    result.add(nowroot.right);
                size = size-1;//
            }
            height += 1;//高度加1
        }
        return height;
    }
}

二叉树任意两个节点之间路径的最大长度

考察点：树

int maxDist(Tree root) { 
    //如果树是空的，则返回0  
    if(root == NULL) 
        return 0; 
    if(root->left != NULL) { 
        root->lm = maxDist(root->left) +1; 
    } 
    if(root->right != NULL) 
        root->rm = maxDist(root->right) +1; 
    //如果以该节点为根的子树中有最大的距离，那就更新最大距离  
    int sum = root->rm + root->lm; 
    if(sum > max) { 
        max = sum; 
    } 

    return root->rm > root->lm ?root->rm : root->lm; 
}

算法题：二叉树层序遍历，进一步提问：要求每层打印出一个换行符

考察点：二叉树

public
List<List<Integer>> levelOrder(TreeNode root) {
           // 存最终结果
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        // 队列
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        if (root == null) {
            return result;
        }
        queue.offer(root);
           // 层次遍历
        while (queue.size() != 0) {
            List<Integer> temp = new ArrayList<Integer>();
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode temp = queue.poll();
                temp.add(temp.val);
                // 左右子树是否为空
                if (temp.left != null) {
                    queue.offer(temp.left);
                }
                if (temp.right != null) {
                    queue.offer(temp.right);
                }
            }
             result.add(temp);
        }
        return result;
}

怎么求一个二叉树的深度?手撕代码?

考察点：二叉树

类似上面求二叉树的深度的题，这里给出递归的方式。

public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root==null) 
            return 0;
        int left = TreeDepth(root.left);
        int right = TreeDepth(root.right);
        return (left>right)?(left+1):(right+1);
    }
}

请你说一下，B+树和B-树？

考察点：树

参考回答：

B+树内节点不存储数据，所有 data 存储在叶节点导致查询时间复杂度固定为 log n。而B-树查询时间复杂度不固定，与 key 在树中的位置有关，最好为O(1)。
B+树叶节点两两相连可大大增加区间访问性，可使用在范围查询等，而B-树每个节点 key 和 data 在一起，则无法区间查找。
B+树更适合外部存储。由于内节点无 data 域，每个节点能索引的范围更大更精确

补充：二叉树/B树/B+树/红黑树

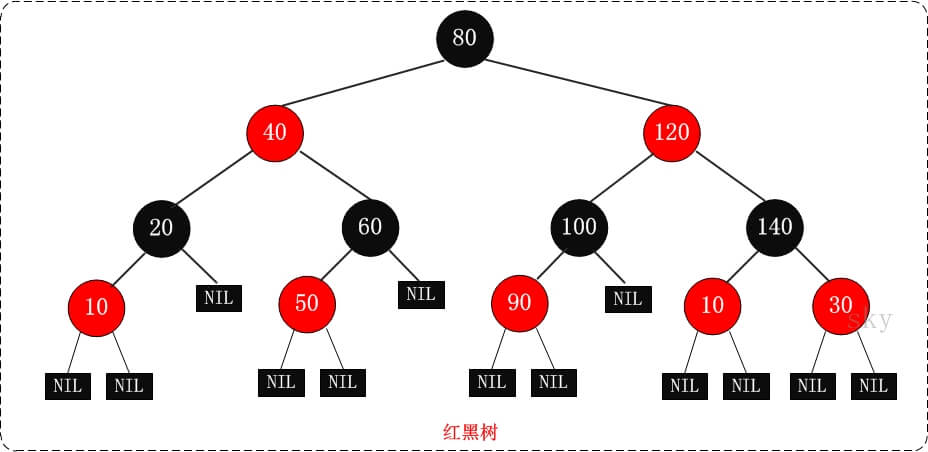
红黑树 R-B Tree ：自平衡二叉树

在每个节点增加了一个存储位记录节点的颜色，可以是 RED，也可以是 BLACK，

通过任意一条从根到叶子简单路径上颜色的约束，红黑树保证最长路径不超过最短路径的两倍，加以平衡。

在二叉查找树基础上，添加以下性质:

节点是红色或黑色

根节点是黑色

每个为空的叶子节点是黑色的

每个红色节点的两个子节点都是黑色

从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点

时间复杂度为O（logn）

B-tree （B树）：多路搜索树

文件系统和数据库的索引都是存在硬盘上的，并且如果数据量大的话，不一定能一次性加载到内存中。

如果在内存中，红黑树比B树效率更高，但是涉及到磁盘操作，B树就更优了。

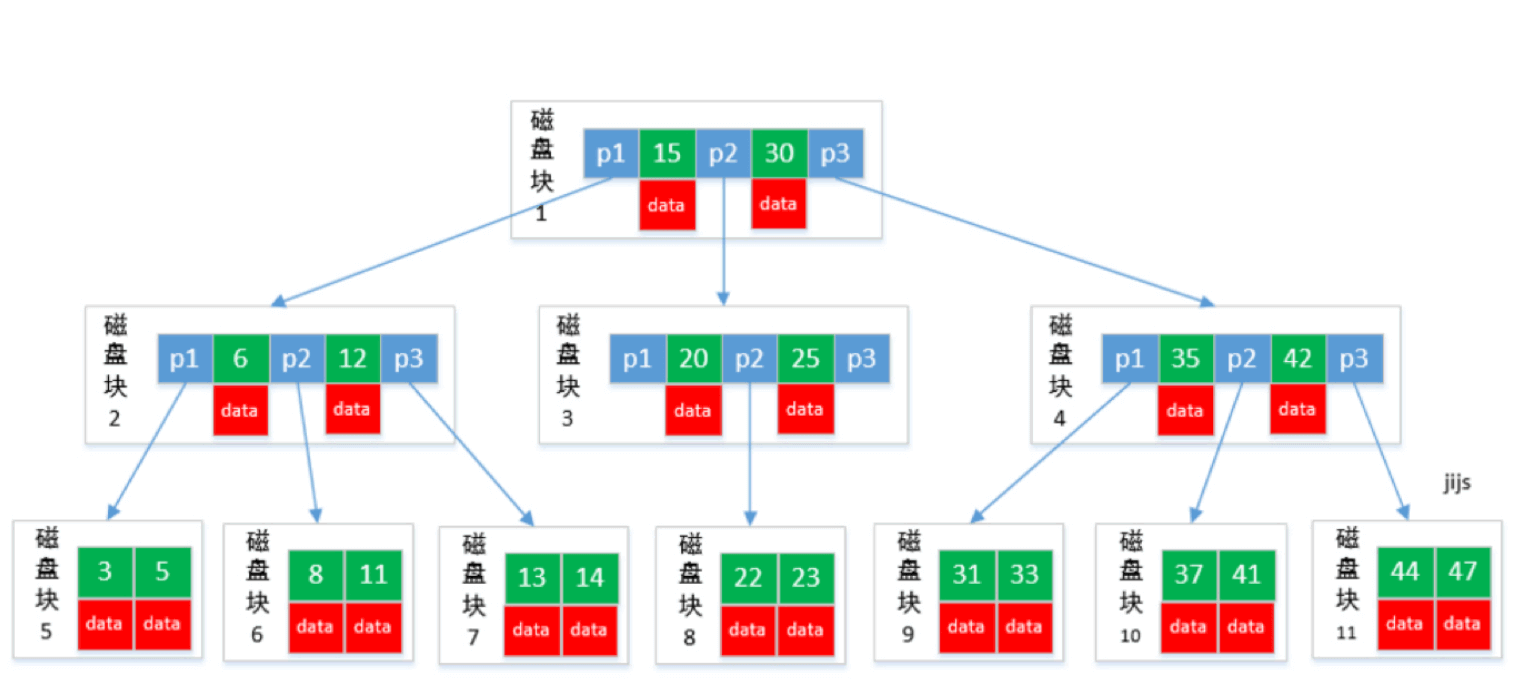
B-tree 利⽤了磁盘块的特性进⾏构建的树。每个磁盘块⼀个节点，每个节点包含了很多关键字。把树的节点关键字增多后树的层级⽐原来的⼆叉树少了，减少数据查找的次数和复杂度。

B-tree巧妙利⽤了磁盘预读原理，将⼀个节点的⼤⼩设为等于⼀个⻚（每⻚为4K），这样每个节点只需要⼀次I/O就可以完全载⼊。

B-tree 的数据可以存在任何节点中。

B+tree

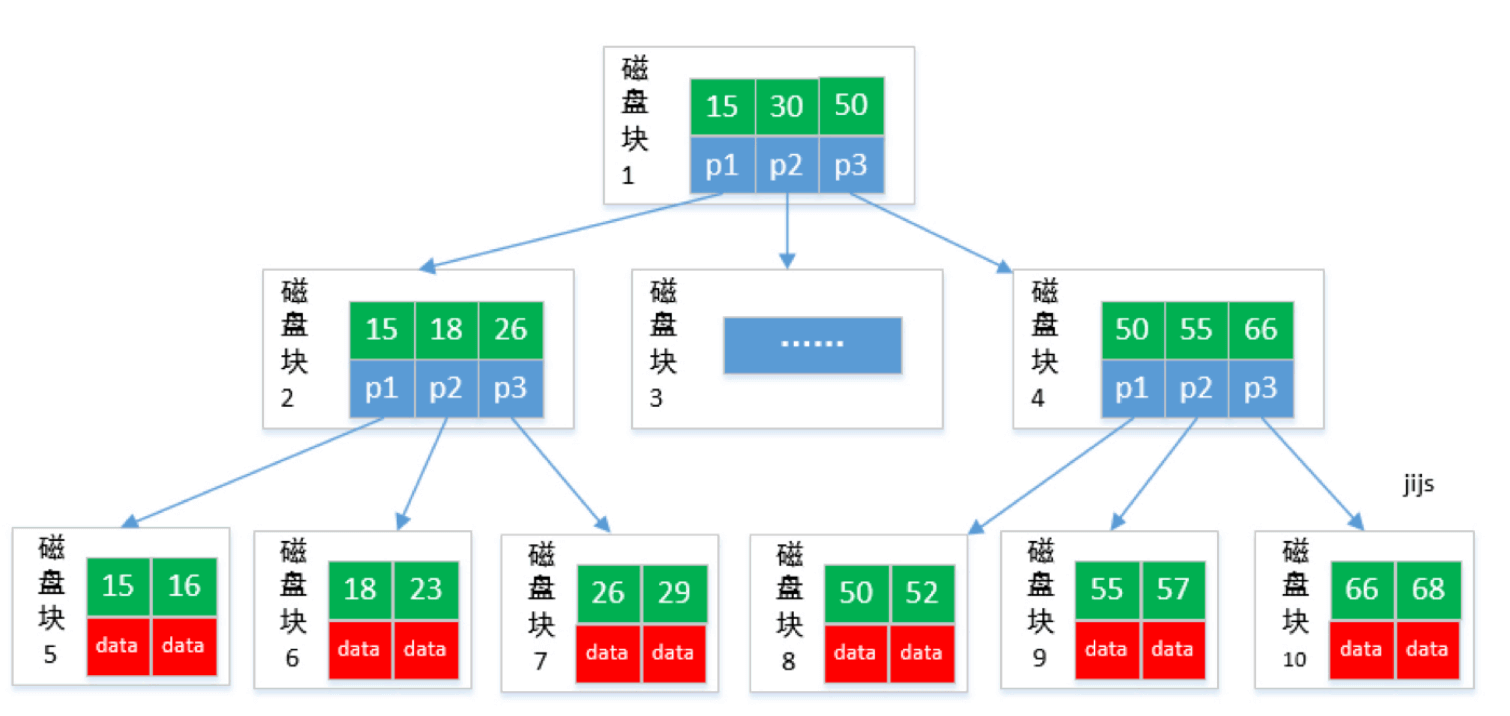
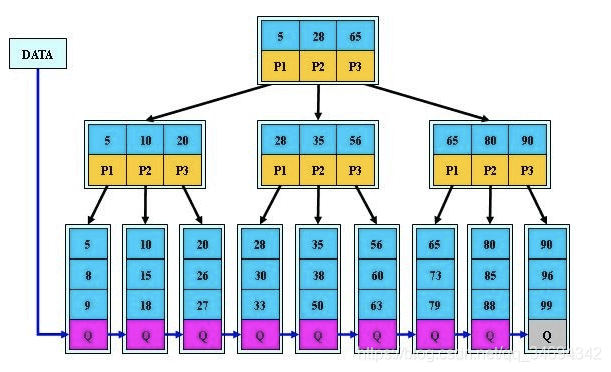
B+tree 是 B-tree 的变种，B+tree 数据只存储在叶⼦节点中。这样在B树的基础上每个节点存储的关键字数更多，树的层级更少所以查询数据更快，所有指关键字指针都存在叶⼦节点，所以每次查找的次数都相同所以查询速度更稳定;

详见：https://www.cnblogs.com/rainwang/p/12243954.html（漫画形式）

https://blog.csdn.net/qq_34694342/article/details/84255739

https://www.sohu.com/a/154640931_478315（漫画形式）

链表

现在有一个单向链表，谈一谈，如何判断链表中是否出现了环

考察点：链表

参考回答：

单链表有环，是指单链表中某个节点的next指针域指向的是链表中在它之前的某一个节点，这样在链表的尾部形成一个环形结构。

解法：定义两个指针，同时从链表的头节点出发，一个指针一次走一步，另一个指针一次走两步。如果走得快的指针追上了走得慢的指针，那么链表就是环形链表；如果走得快的指针走到了链表的末尾（next指向 NULL）都没有追上第一个指针，那么链表就不是环形链表。

谈一谈，bucket如果用链表存储，它的缺点是什么？

考察点：链表

参考回答：

①查找速度慢，因为查找时，需要循环链表访问

②如果进行频繁插入和删除操作，会导致速度很慢。

有一个链表，奇数位升序偶数位降序，如何将链表变成升序

考察点：链表

思路：将链表按照奇偶数位分成两个链表head1和head2，如1->6->3->4->5->2，得到1->3->5和6->4->2两个链表，将6->4->2反转得到2->4->6，在将两个链表合并。

public class
OddIncreaseEvenDecrease {
    /**
     * 按照奇偶位拆分成两个链表
     * @param head
     * @return
     */
    // 例子 1 6 3 4 5 2 变成 1 2 3 4 5 6
    public static Node[] getLists(Node head){
        Node head1 = null;
        Node head2 = null;

        Node cur1 = null;
        Node cur2 = null;
        int count = 1;//用来计数
        while(head != null){
            // 遇到1 3 5 
            if(count % 2 == 1){
                if(cur1 != null){
                    cur1.next = head;
                    cur1 = cur1.next;
                }else{
                    cur1 = head;
                    head1 = cur1;
                }
            }else{
                if(cur2 != null){
                    cur2.next = head;
                    cur2 = cur2.next;
                }else{
                    cur2 = head;
                    head2 = cur2;
                }
            }
            head = head.next;
            count++;
        }
        //跳出循环，要让最后两个末尾元素的下一个都指向null
        cur1.next = null;
        cur2.next = null;

        Node[] nodes = new Node[]{head1,head2};
        return nodes;
    }

    /**
     * 反转链表
     * @param head
     * @return
     */
    public static Node reverseList(Node head){
        Node pre = null;
        Node next = null;
        while(head != null){
            next = head.next;
            head.next = pre;
            pre = head;
            head = next;
        }
        return pre;
    }

    /**
     * 合并两个有序链表
     * @param head1
     * @param head2
     * @return
     */
    public static Node CombineList(Node head1,Node head2){
        if(head1 == null || head2 == null){
            return head1 != null ? head1 :head2;
        }
        Node head = head1.value < head2.value ?head1 : head2;
        Node cur1 = head == head1 ? head1 :head2;
        Node cur2 = head == head1 ? head2 :head1;
        Node pre = null;
        Node next = null;
        while(cur1 != null && cur2 !=null){
            if(cur1.value <= cur2.value){//这里一定要有=，否则一旦cur1的value和cur2的value相等的话，下面的pre.next会出现空指针异常
                pre = cur1;
                cur1 = cur1.next;
            }else{
                next = cur2.next;
                pre.next = cur2;
                cur2.next = cur1;
                pre = cur2;
                cur2 = next;
            }
        }
        pre.next = cur1 == null ? cur2 : cur1;

        return head;
    }

}

随机链表的复制

考察点：链表

public RandomListNode copyRandomList(RandomListNode head) {

    if (head == null)
        return null;

    RandomListNode p = head;

    // copy every node and insert to list
    while (p != null) {
        RandomListNode copy = new RandomListNode(p.label);
        copy.next = p.next;
        p.next = copy;
        p = copy.next;
    }

    // copy random pointer for each new node
    p = head;
    while (p != null) {
        if (p.random != null)
            p.next.random = p.random.next;
        p = p.next.next;
    }

    // break list to two
    p = head;
    RandomListNode newHead = head.next;
    while (p != null) {
        RandomListNode temp = p.next;
        p.next = temp.next;
        if (temp.next != null)
            temp.next = temp.next.next;
        p = p.next;
    }

    return newHead;
}

如何反转单链表

考察点：链表

public static Node reverseList(ListNode head){
    ListNode pre = null;
    ListNode next = null;
    while(head != null){
        next = head.next;
        head.next = pre;
        pre = head;
        head = next;
    }
    return pre;
}

数组

写一个算法，可以将一个二维数组顺时针旋转90度，说一下思路。

考察点：数组

public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n/2; i++) {
            for (int j = i; j < n-1-i; j++)
{
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n-1-j][i];
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
                matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
                matrix[j][n-1-i] = temp;
            }
        }
}

一个数组，除一个元素外其它都是两两相等，求那个元素?

考察点：数组

解法：位运算，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

 public static int find1From2(int[] a){
        int len = a.length, result = 0;
        for(int i = 0; i < len; i++){
            result = result ^ a[i];
        }
        return result;
}

找出数组中和为S的一对组合，找出一组就行

考察点：数组

解法：两数之和经典题，找到一组即可返回，使用HashMap即可。

public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
        int[] a = new int[2];
        map.put(nums[0], 0);
        for (int i = 1; i < nums.length;i++) {
            if (map.containsKey(target - nums[i])) {
                a[0] = map.get(target - nums[i]);
                a[1] = i;
                return a;
            } else {
                map.put(nums[i], i);
            }
        }
        return a;
}

求一个数组中连续子向量的最大和

考察点：数组

public int maxSubArray(int[] nums) {
        int sum = 0;
        int maxSum = Integer.MIN_VALUE;
        if (nums == null || nums.length == 0) {
            return sum;
        }
        for (int i = 0; i < nums.length;i++) {
            sum += nums[i];
            maxSum = Math.max(maxSum, sum);
            if (sum < 0) {
                sum = 0;
            }
        }
        return maxSum;
}

寻找一数组中前K个最大的数

考察点：数组

解法：考场排序，可以用堆排序，也可以用快排，面试的时候看面试官怎么要求。这里给出快排的解法，自己也可以尝试其他的方法。

public int findKthLargest(int[] nums, int k) {
    if (k < 1 || nums == null) {
        return 0;
    }
    return getKth(nums.length - k +1, nums, 0,nums.length - 1);
}
 // 快排模板
public int getKth(int k, int[] nums, int start, int end) {
    int pivot = nums[end];
    int left = start;
    int right = end;
    while (true) {
        while(nums[left] < pivot && left < right) {
            left++;
        }
        while(nums[right] >= pivot && right > left) {
            right--;
        }

        if(left == right) {
            break;
        }

        swap(nums,left, right);
    }
    swap(nums, left, end);
    if (k == left + 1) {
        return pivot;
    } else if (k < left + 1) {
        return getKth(k, nums, start, left - 1);
    } else {
        return getKth(k, nums, left + 1, end);
    }
}
// 交换元素值
public void swap(int[] nums, int n1, int n2) {
    int tmp = nums[n1];
    nums[n1] = nums[n2];
    nums[n2] = tmp;
}

排序

用java写一个冒泡排序？

考察点：冒泡排序

public static void main(String[] args) {
    int[] result = {2,4,1,3,6,5};
    int temp;
    System.out.println("----冒泡排序前顺序----");
    for (int i : result) {
        System.out.print(i);
    }
    for(int i=0;i<result.length-1;i++){
        for(int j = 0;j<result.length-1-i;j++){
            if(result[j+1]<result[j]){
                //后一个比前一个小
                temp = result[j];
                result[j] = result[j+1];
                result[j+1] = temp;
            }
        }
    }
    System.out.println();
    System.out.println("----冒泡排序后结果----");
    for (int i : result) {
        System.out.print(i);
    }
}

介绍一下，排序都有哪几种方法？请列举出来。

考察点：排序

参考回答：

排序的方法有：

插入排序（简单插入排序、希尔排序）

交换排序（冒泡排序、快速排序）

选择排序（简单选择排序、堆排序）

归并排序

分配排序（箱排序、基数排序）

绍一下，归并排序的原理是什么？

考察点：归并排序

参考回答：

（1）归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

（2）首先考虑下如何将将二个有序数列合并。这个非常简单，只要从比较二个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。

（3）解决了上面的合并有序数列问题，再来看归并排序，其的基本思路就是将数组分成二组A，B，如果这二组组内的数据都是有序的，那么就可以很方便的将这二组数据进行排序。如何让这二组组内数据有序了？

可以将A，B组各自再分成二组。依次类推，当分出来的小组只有一个数据时，可以认为这个小组组内已经达到了有序，然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列，再合并数列就完成了归并排序。

介绍一下，堆排序的原理是什么？

考察点：堆排序

参考回答：

堆排序分大顶堆和小顶堆，这里以大顶堆为例讲解。

堆排序就是把最大堆堆顶的最大数取出，将剩余的堆继续调整为最大堆，再次将堆顶的最大数取出，这个过程持续到剩余数只有一个时结束。在堆中定义以下几种操作：

（1）最大堆调整（Max-Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点。

（2）创建最大堆（Build-Max-Heap）：将堆所有数据重新排序，使其成为最大堆。

（3）堆排序（Heap-Sort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

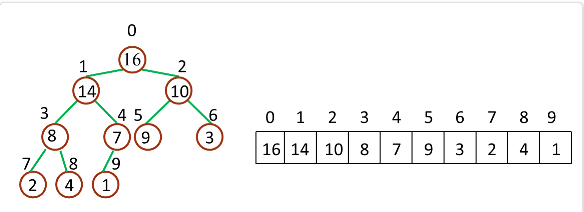
谈一谈，如何得到一个数据流中的中位数？

考察点：排序

参考回答：

数据是从一个数据流中读出来的，数据的数目随着时间的变化而增加。如果用一个数据容器来保存从流中读出来的数据，当有新的数据流中读出来时，这些数据就插入到数据容器中。

数组是最简单的容器。如果数组没有排序，可以用 Partition 函数找出数组中的中位数。在没有排序的数组中插入一个数字和找出中位数的时间复杂度是 O(1)和 O(n)。

我们还可以往数组里插入新数据时让数组保持排序，这是由于可能要移动 O(n)个数，因此需要 O(n)时间才能完成插入操作。在已经排好序的数组中找出中位数是一个简单的操作，只需要 O(1)时间即可完成。

排序的链表时另外一个选择。我们需要 O(n)时间才能在链表中找到合适的位置插入新的数据。如果定义两个指针指向链表的中间结点（如果链表的结点数目是奇数，那么这两个指针指向同一个结点），那么可以在 O（1）时间得出中位数。此时时间效率与及基于排序的数组的时间效率一样。

如果能够保证数据容器左边的数据都小于右边的数据，这样即使左、右两边内部的数据没有排序，也可以根据左边最大的数及右边最小的数得到中位数。如何快速从一个容器中找出最大数？用最大堆实现这个数据容器，因为位于堆顶的就是最大的数据。同样，也可以快速从最小堆中找出最小数。

因此可以用如下思路来解决这个问题：用一个最大堆实现左边的数据容器，用最小堆实现右边的数据容器。往堆中插入一个数据的时间效率是 O(logn)。由于只需 O(1)时间就可以得到位于堆顶的数据，因此得到中位数的时间效率是 O(1)。

你知道哪些排序算法，这些算法的时间复杂度分别是多少，解释一下快排？

考察点：快排

参考回答：

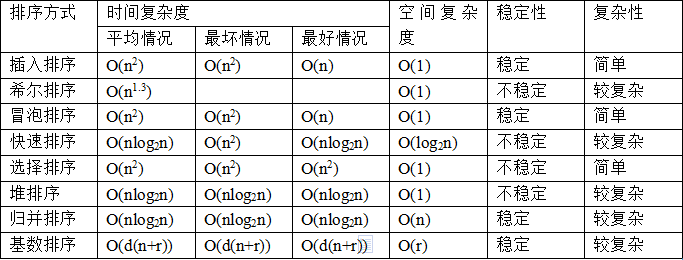
快排：快速排序有两个方向，左边的i下标一直往右走（当条件a[i] <= a[center_index]时），其中center_index是中枢元素的数组下标，一般取为数组第0个元素。

而右边的j下标一直往左走（当a[j] > a[center_index]时）。

如果i和j都走不动了，i <= j, 交换a[i]和a[j],重复上面的过程，直到i>j。交换a[j]和a[center_index]，完成一趟快速排序。

遍历

二叉树 Z 字型遍历

考察点：遍历

import java.util.*;
public class Solution {
    public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        //标记奇偶层 开始为0层 从左->右遍历
        boolean flag = true;
        if (pRoot == null) {
            return result;
        }
        queue.add(pRoot);
        while (queue.size() != 0) {
            flag = !flag;
            int size = queue.size();
            ArrayList<Integer> temp = new ArrayList<Integer>();
            for (int i = 0; i < size; i++) {
                TreeNode curroot = queue.poll();
                temp.add(curroot.val);
                if (curroot.left != null) 
                    queue.add(curroot.left);
                if (curroot.right != null)
                    queue.add(curroot.right);
            }
            // 反转
            if (flag) {
                Collections.reverse(temp);
            }
            result.add(temp);
        }
        return result;
    }
}

编程题：写一个函数，找到一个文件夹下所有文件，包括子文件夹

考察点：遍历

import java.io.File;
public class Counter2 {
    public static void main(String[] args) {
        //取得目标目录
        File file = new File("D:");
        //获取目录下子文件及子文件夹
        File[] files = file.listFiles();
        readfile(files);
    }

    public static void readfile(File[] files) {
        if(files == null) {// 如果目录为空，直接退出  
            return; 
        }
        for(File f:files) {
            //如果是文件，直接输出名字
            if(f.isFile()) {
                System.out.println(f.getName());
            }
            //如果是文件夹，递归调用
            else if(f.isDirectory()) {
                readfile(f.listFiles());
            }
        }
    }
}

堆栈

请你解释一下，内存中的栈(stack)、堆(heap) 和静态区(static area) 的用法。

考察点：堆栈

参考回答：

**堆区:**专门用来保存对象的实例(new 创建的对象和数组)，实际上也只是保存对象实例的属性值，属性的类型和对象本身的类型标记等，并不保存对象的方法（方法是指令，保存在Stack中）

存储的全部是对象，每个对象都包含一个与之对应的class的信息。(class的目的是得到操作指令)
jvm只有一个堆区(heap)被所有线程共享，堆中不存放基本类型和对象引用，只存放对象本身.
一般由程序员分配释放，若程序员不释放，程序结束时可能由OS回收。

**栈区:**对象实例在Heap 中分配好以后，需要在Stack中保存一个4字节的Heap内存地址，用来定位该对象实例在Heap 中的位置，便于找到该对象实例。

每个线程包含一个栈区，栈中只保存基础数据类型的对象和自定义对象的引用(不是对象)，对象都存放在堆区
每个栈中的数据(原始类型和对象引用)都是私有的，其他栈不能访问。
栈分为3个部分：基本类型变量区、执行环境上下文、操作指令区(存放操作指令)。
由编译器自动分配释放，存放函数的参数值，局部变量的值等．

静态区/方法区:

方法区又叫静态区，跟堆一样，被所有的线程共享。方法区包含所有的class和static变量。
方法区中包含的都是在整个程序中永远唯一的元素，如class，static变量。
全局变量和静态变量的存储是放在一块的，初始化的全局变量和静态变量在一块区域，未初始化的全局变量和未初始化的静态变量在相邻的另一块区域

说一说，heap和stack有什么区别。

考察点：堆与栈

参考回答：

1.heap是堆，stack是栈。
2.stack的空间由操作系统自动分配和释放，heap的空间是手动申请和释放的，heap常用new关键字来分配。
3.stack空间有限，heap的空间是很大的自由区。在Java中，若只是声明一个对象，则先在栈内存中为其分配地址空间，若再new一下，实例化它，则在堆内存中为其分配地址。
4.举例：数据类型变量名；这样定义的东西在栈区。如：Object a =null; 只在栈内存中分配空间new 数据类型();或者malloc(长度); 这样定义的东西就在堆区如：Object b =new Object(); 则在堆内存中分配空间

介绍一下，堆与栈的不同是什么？

考察点：堆，栈

参考回答：

（1）Java的堆是一个运行时数据区，类的对象从中分配空间。通过比如：new等指令建立，不需要代码显式的释放，由垃圾回收来负责。

优点：可以动态地分配内存大小，垃圾收集器会自动回收垃圾数据。

缺点：由于其优点，所以存取速度较慢。

（2）栈：

其数据项的插入和删除都只能在称为栈顶的一端完成，后进先出。栈中存放一些基本类型的变量和对象句柄。

优点：读取数度比堆要快，仅次于寄存器，栈数据可以共享。

缺点：比堆缺乏灵活性，存在栈中的数据大小与生存期必须是确定的。

举例：

String是一个特殊的包装类数据。可以用：
String str = new String(“csdn”);
String str = “csdn”;

两种的形式来创建，第一种是用new()来新建对象的，它会在存放于堆中。每调用一次就会创建一个新的对象。而第二种是先在栈中创建一个对String类的对象引用变量str，然后查找栈中有没有存放”csdn”，如果没有，则将”csdn”存放进栈，并令str指向”abc”，如果已经有”csdn” 则直接令str指向“csdn”。

队列

什么是Java优先级队列(Priority Queue)？

考察点：队列

参考回答：

PriorityQueue是一个基于优先级堆的无界队列，它的元素是按照自然顺序(natural order)排序的。在创建的时候，可以给它提供一个负责给元素排序的比较器。PriorityQueue不允许null值，因为他们没有自然顺序，或者说他们没有任何的相关联的比较器。最后，PriorityQueue不是线程安全的，入队和出队的时间复杂度是O(log(n))。

高级算法

请你讲讲LRU算法的实现原理？

考察点：LRU算法

参考回答：

注意：面试可能会让手写LRU算法！

①LRU（Least recently used，最近最少使用）算法根据数据的历史访问记录来进行淘汰数据，其核心思想是“如果数据最近被访问过，那么将来被访问的几率也很高”，反过来说“如果数据最近这段时间一直都没有访问,那么将来被访问的概率也会很低”，两种理解是一样的；常用于页面置换算法，为虚拟页式存储管理服务。

②达到这样一种情形的算法是最理想的：每次调换出的页面是所有内存页面中最迟将被使用的；这可以最大限度的推迟页面调换，这种算法，被称为理想页面置换算法。可惜的是，这种算法是无法实现的。

为了尽量减少与理想算法的差距，产生了各种精妙的算法，最近最少使用页面置换算法便是其中一个。LRU 算法的提出，是基于这样一个事实：在前面几条指令中使用频繁的页面很可能在后面的几条指令中频繁使用。反过来说，已经很久没有使用的页面很可能在未来较长的一段时间内不会被用到。这个，就是著名的局部性原理——比内存速度还要快的cache，也是基于同样的原理运行的。因此，我们只需要在每次调换时，找到最近最少使用的那个页面调出内存。

LRU主要的两个函数 获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果关键字 (key) 存在于缓存中，则获取关键字的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字/值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

算法实现的关键

命中率：当存在热点数据时，LRU的效率很好，但偶发性的、周期性的批量操作会导致 LRU 命中率急剧下降，缓存污染情况比较严重。
复杂度：实现起来较为简单。
存储成本：几乎没有空间上浪费。
代价：命中时需要遍历链表，找到命中的数据块索引，然后需要将数据移到头部。

为什么要设计后缀表达式，有什么好处？

考察点：逆波兰表达式

参考回答：

后缀表达式又叫逆波兰表达式，逆波兰记法不需要括号来标识操作符的优先级。

请你设计一个算法，用来压缩一段URL？

考察点：MD5加密算法

参考回答：

该算法主要使用MD5 算法对原始链接进行加密（这里使用的MD5 加密后的字符串长度为32 位），然后对加密后的字符串进行处理以得到短链接的地址。

谈一谈，id全局唯一且自增，如何实现？

考察点：SnowFlake雪花算法

参考回答；

SnowFlake雪花算法

雪花ID生成的是一个64位的二进制正整数，然后转换成10进制的数。64位二进制数由如下部分组成：

snowflake id生成规则

1位标识符：始终是0，由于long基本类型在Java中是带符号的，最高位是符号位，正数是0，负数是1，所以id一般是正数，最高位是0。
41位时间戳：41位时间截不是存储当前时间的时间截，而是存储时间截的差值（当前时间截 - 开始时间截 )得到的值，这里的的开始时间截，一般是我们的id生成器开始使用的时间，由我们程序来指定的。
10位机器标识码：可以部署在1024个节点，如果机器分机房（IDC）部署，这10位可以由 5位机房ID + 5位机器ID 组成。
12位序列：毫秒内的计数，12位的计数顺序号支持每个节点每毫秒(同一机器，同一时间截)产生4096个ID序号

优点

简单高效，生成速度快。
时间戳在高位，自增序列在低位，整个ID是趋势递增的，按照时间有序递增。
灵活度高，可以根据业务需求，调整bit位的划分，满足不同的需求。

缺点

依赖机器的时钟，如果服务器时钟回拨，会导致重复ID生成。
在分布式环境上，每个服务器的时钟不可能完全同步，有时会出现不是全局递增的情况。

Design and implement a data structure for Least Frequently Used (LFU) cache. It should support the following operations: get and put. get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1. put(key, value) - Set or insert the value if the key is not already present. When the cache reaches its capacity, it should invalidate the least frequently used item before inserting a new item. For the purpose of this problem, when there is a tie (i.e., two or more keys that have the same frequency), the least recently used key would be evicted. Could you do both operations in O(1) time complexity?

考察点：LFU Cache

public class LFUCache {
private class Node{
    int value;
    ArrayList<Integer> set;
    Node prev;
    Node next;
    public Node (int value ){
        this.value = value;
        this.set = new ArrayList<Integer> ();
        this.prev = null;
        this.next = null;
    }
}
private class item{
    int key;
    int value;
    Node parent ;
    public item(int key ,int value, Node parent){
         this.key = key ;
         this.value = value;
         this.parent  = parent;
    }
}
private HashMap<Integer, item> map;
private  Node head,tail;
private  int capacity;
// @param capacity, an integer
public LFUCache(int capacity) {
    // Write your code here
    this.capacity = capacity;
    this.map = new HashMap <Integer,item> ();
    this.head = new Node (0);
    this.tail = new Node(Integer.MAX_VALUE);
    head.next = tail;
    tail.prev = head;


}
// @param key, an integer
// @param value, an integer
// @return nothing
public void set(int key, int value) {
    // Write your code here
   if (get(key) != -1 ) {
      map.get(key).value = value;
      return ;
   }
   if (map.size() == capacity ){
       getLFUitem();
   }

   Node newpar = head.next;
   if ( newpar.value != 1){
       newpar = getNewNode(1,head,newpar);
   }
    item curitem = new item(key,value,newpar);
    map.put(key,curitem);
    newpar.set.add(key);
    return;  
}
public int get(int key) {
    // Write your code here
    if (!map.containsKey(key)){
        return -1;
    }
    item cur = map.get(key);
    Node curpar = cur.parent;
    if (curpar.next.value == curpar.value + 1){
        cur.parent= curpar.next;
        cur.parent.set.add(key);
    }else{
        Node newpar =getNewNode(curpar.value + 1,curpar,curpar.next);
        cur.parent = newpar;
        newpar.set.add(key);
    }
     curpar.set.remove(new Integer(key));
     if(curpar.set.isEmpty()){
         deleteNode(curpar);
     }
    return cur.value;
}
private Node getNewNode (int value ,Node prev , Node next){
    Node temp = new Node(value);
    temp.prev = prev;
    temp.next = next;
    prev.next = temp;
    next.prev = temp;
    return temp;
}
private void deleteNode(Node temp){
    temp.prev.next = temp.next;
    temp.next.prev = temp.prev;
    return ;
}
private void getLFUitem(){
    Node temp = head.next;
    int LFUkey = temp.set.get(0);
    temp.set.remove(0);
    map.remove(LFUkey);
    if (temp.set.isEmpty()){
        deleteNode(temp);
    }
    return;
}

来源：https://www.nowcoder.com/tutorial/94/ea1986fcff294f6292385703e94689e8